ピタゴラスの定理は、直角三角形の脚の四角形の合計は斜辺(直角の反対側)の四角形に等しいと述べています-よく知られた代数表記では、a 2 + b 2 = c 2。エジプト人は、この関係を満たす整数のトリプル(a、b、c)をいくつか見つけました。ピタゴラス(紀元前580〜紀元前500年)またはその信者の1人が、彼の名前が付いた定理を最初に証明した可能性があります ユークリッド(紀元前300年頃)は、図形の形状からの風車証明として知られている要素で、ピタゴラスの定理の巧妙なデモンストレーションを提供しました。
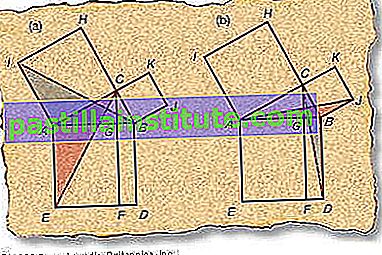
- 右Δの両側に四角形を描画A B C。
- B C H及びA C Kは ∠ので、直線であるA 、C B = 90°。
- ∠ E A B =∠ C A I = 90°、構造によって。
- ∠ B A I =∠ B A C +∠ C A I =∠ B A C +∠ E A B =∠ E A C 3によって、。
- A C = A IおよびA B = A E、構造による。
- したがって、Δ B A I ≅Δ E A Cは、()図の一部で強調表示されるよう、:、側角側定理により(ロバの橋サイドバーを参照します)。
- B Dに平行にC Fを描きます。
- 長方形A G F E =2Δ A C E。この注目すべき結果は、2つの予備的な定理から導き出されます。(b)三角形の面積は、底面と高さが同じ平行四辺形(長方形を含む)の半分です。
- 正方形A I H C =2Δ B A I、ステップ8と同様平行四辺形定理によって、。
- したがって、ステップ6、8、および9によって、長方形A G F E =正方形A I H Cになります。
- ∠ D B C =∠ A B Jステップ3及び4のように、。
- B C = B JおよびB D = A B、手順5と同様の構成。
- Δ C B D ≅Δ J B A、ステップ6のように図の(B)に強調しました。
- 矩形B D F G =2Δ C B Dステップ8と同様に、。
- 正方形C K J B =2Δ J B Aステップ9でのように、。
- したがって、ステップ10のように、長方形B D F G =正方形C K J Bです。
- 正方形A B D E =長方形A G F E +長方形B D F G、構造による。
- したがって、正方形A B D E =正方形A I H C +正方形C K J Bは、ステップ10と16によって計算されます。
ユークリッドの要素の最初の本点の定義で始まり、ピタゴラスの定理とその逆で終わります(三角形の2つの辺の正方形の合計が3番目の辺の正方形と等しい場合、それは直角三角形でなければなりません)。特定の定義から抽象的で普遍的な数学的記述へのこの旅は、文明化された生命の発展の象徴として受け取られてきました。ユークリッドの推論の最高の表現による識別の顕著な例は、ドイツの物理学者であり天文学者によって火星の住民と彼らに知的成熟への私たちの主張を示すことによって会話を開くように提案した1821年の提案でした。彼らの興味と承認を引き付けるために私たちがしなければならなかったすべては、風車図の形で、または他の人が提案したように、大きな畑を耕して植えることでしたシベリアまたはサハラのピタゴラスの定理を連想させる運河を掘り、油で満たし、火にかけ、反応を待つために。実験は行われておらず、火星の住民が望遠鏡も幾何学も存在もしていないかどうかは未定のままです。